050 – COMSOL七个表面等离激元教学型案例（只有模型文件）

基本介绍：

• 主要内容：根据S. A. Maier所著的等离子体光学书《Plasmonics: Fundamentals and applications》，精选了书中7个关于传播型表面等离极化激元（SPP）的重要模型，做成了COMSOL案例（即本例支付70元获得7个comsol模型）；
• 基于 COMSOL 频域求解，使用的软件版本为 COMSOL 5.3 (5.3.0.223)；
• 计算所需的内存：4 GB；
• 涉及的内容：全局参数、用三种方法来定义Drude模型、周期性条件、完美匹配层、自定义网格、端口、边界模式分析、散射边界条件、远场域、绘图的高度表达式 等；
• 绘制了：电场分布、磁场分布、透射率、反射率、SPP的色散曲线、远场光强 等；
• 注意：本案例仅包含模型文件，没有讲解视频。购买此案例不附带答疑指导。

包含的文件截图：

计算的内容和结果：

（1）金属对横电磁波“透明”的模拟。这个文件中计算了三种不同频率的入射光照射到金属上的反射或透射现象。金属用Drude模型来定义，为了方便展示效果，Drude模型的参数是特意凑好的，而非代表现实中的某种特定金属。计算表明：当光的角频率（ω）低于等离子体频率（ω_p）时，光无法透过金属；当ω高于ω_p时，光能够透过金属，相当于金属透明了。下图展示了频率分别为0.6倍、1.0倍和1.4倍等离子体频率的电磁波，由空气正射入金属时的电场分布 👇

（2）导体-介质界面的表面等离激元。这个文件中的金属用Drude模型来定义，环境是空气。计算了表面等离激元（SPP）的磁场分布和色散曲线 👇

（3）导体-介质-导体（MIM）的表面等离激元耦合。金属使用Drude模型，模拟导体-介质-导体间表面等离激元的耦合情况，同时计算了奇偶两种模式的电磁场分布 👇

（4）介质-导体-介质(IMI)的表面等离激元耦合。金属使用Drude模型，模拟介质-导体-介质间表面等离激元的耦合情况，同时展示奇偶两种模式的电磁场分布 👇

（5）棱镜耦合法激发表面等离激元。为了在金属-介质界面处激发SPPs，一种常用的方法是棱镜耦合。棱镜耦合有两种方式，分别为Kretschmann型和Otto型。以Kretschmann型为例，在棱镜表面覆盖一层金属薄膜，电磁波从棱镜一侧以θ角度入射到金属薄膜上。当满足波矢匹配时，SPPs能够在金属-空气界面处激发出来。本例分别用高斯光和平面光来激发SPP 👇

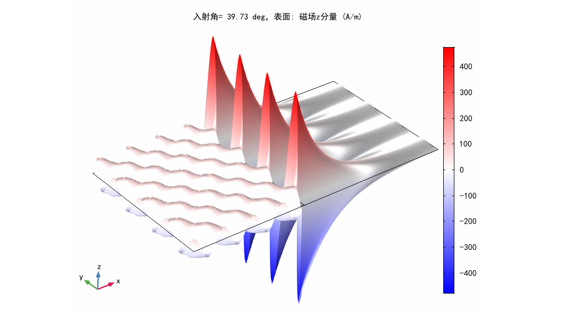
（6）光栅耦合法激发SPPs。在金属-介质界面处激发表面等离激元（SPPs）的另一种常用的方法是光栅耦合。金属使用Drude模型，用TM偏振的高斯光入射，在入射角合适时（满足波矢匹配），能够激发出表面等离激元。本例分别用高斯光和平面光来激发SPP 👇

（7）利用漏辐射测量SPPs。对于介质-金属-介质的结构，如果两侧介质的折射率不同，且表面等离激元（SPPs）在低折射率介质一侧传播，当金属膜较薄时，SPPs的能量会透过金属膜而漏到高折射率一侧。漏到高折射率一侧的电磁波以空间电磁波形式辐射出去，被称为“漏辐射（leakage radiation）”。测量漏辐射的辐射方向角分布，就可以推算出SPP的某些性质。本例中，低折射率介质为空气，高折射率介质为玻璃（n = 1.45），金属膜使用厚度为50 nm厚的金膜，计算了漏辐射的场分布的辐射方向角远场分布 👇

付费后将能下载模型文件。

再次提醒：本案例仅包含模型文件，没有讲解视频。购买案例不附带答疑指导服务。