075 – COMSOL案例：超表面中等离激元与声子的强耦合（只有模型文件）

基本介绍：

• 主要内容：根据发表在 Optics Express 上的论文《Strong coupling between mid-infrared localized plasmons and phonons（作者：Weiwei Wan等）》，复现了其中的所有内容（Fig. 1c、Fig. 2、Fig. 3b、Fig. 4、Fig. 5ab）；
• 基于 COMSOL 频域求解，使用的软件版本为 COMSOL 6.0 (6.0.0.318)；
• 计算所需的内存：25 GB；
• 涉及的内容：全局参数、自定义变量、Drude色散模型、Lorentz色散模型、端口、周期性条件、自定义网格、参数化扫描、画伪彩图 等；
• 绘制了：反射率随频率变化的曲线、电场分布、强耦合的反交叉曲线；
• 注意：本案例仅包含模型文件，没有讲解视频。购买此案例不附带答疑指导。

包含的文件截图：

详细描述：

如上图所示，在玻璃衬底上镀上一层 50 nm 厚的金膜，然后在金膜上刻蚀出十字形的孔隙，形成超表面。再在金膜上方旋涂一层厚度为 t = 40, 100, 180 nm 的 PMMA 膜（图中未画出）。图中 p = 2.0 ~ 2.8 μm 之间可变，l = 0.8p，w = 0.15p。

沿x方向偏振的平面光从上往下正入射到超表面上，光频率为 40 ~ 80 THz，可以在十字孔中激发出局域表面等离激元共振（LSPR），继而激发出 PMMA 中的声子。等离激元与声子发生强耦合，导致光谱上的拉比（Rabi）劈裂。

在计算中，金的介电常数采用 Drude 模型：

其中 ε_∞ = 1，ω_p = 1.37×10¹⁶ rad/s，γ = 4.08×10¹³ rad/s。PMMA 的介电常数采用 Lorentz 模型：

其中 ε_b = 2.2，ω₀ = 3.269×10¹⁴ rad/s，ε_Lorentz = 0.018，δ = 8.0×10¹¹ rad/s。

计算的内容和结果：

1、不同周期的反射率（左：论文中的 Fig. 1(c)；右：本例的结果）👇

2、“只有超材料/非耦合时/耦合时” 三种情况下的反射率（左：论文中的 Fig. 2；右：本例的结果）👇

3、覆盖了 PMMA 之后，等离激元与声子之间强耦合的反射谱伪彩图（论文中的 Fig. 3(b)；右：本例的结果）👇

4、三种不同 PMMA 厚度对应的耦合系统反射率（左：论文中的 Fig. 4(a)；右：本例的结果）👇

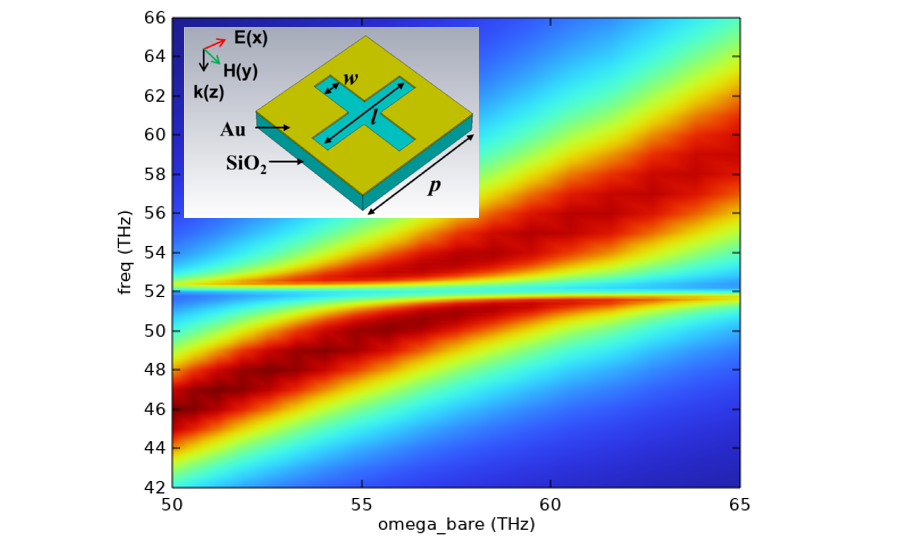
5、PMMA 厚度为 180 nm 时对应的反交叉曲线（左：论文中的 Fig. 4(b)；右：本例的结果）👇

6、PMMA 厚度为 180 nm 时对应的电场分布，(b)图是(a)图中白色虚线上的电场分布（左：论文中的 Fig. 5(a,b)；右：本例的结果）👇

付费后将能下载模型文件。

再次提醒：本案例仅包含模型文件，没有讲解视频。购买案例不附带答疑指导服务。